C阶乘公式是排列组合中的重要公式之一,用于计算从n个不同元素中取出m个元素的组合数,该公式广泛应用于计算机科学、统计学、金融等领域,通过C阶乘公式,可以方便地求解诸如概率计算、事件组合等问题,其应用广泛且实用,是数学领域中的基础工具之一。
在数学的排列组合中,阶乘公式扮演着至关重要的角色,C阶乘公式(组合公式)是我们在处理组合问题时经常使用的工具,本文将详细介绍C阶乘公式的定义、性质、推导及其在各个领域的应用。
排列组合的基本概念
排列和组合是数学中研究事物有序与无序的两种基本方法,排列关注于事物的顺序,而组合则关注于事物的组合方式,不考虑顺序,在实际生活中,排列组合的应用广泛,如统计、概率、计算机科学等。
C阶乘公式的定义与性质
C阶乘公式,也称为组合公式,用于计算从n个不同元素中取出k个元素的组合数,其定义公式为:
C(n, k) = n! / (k!(n-k)!)
n!表示n的阶乘,即n×(n-1)×...×2×1,C(n, k)表示从n个元素中取出k个元素的组合数。
C阶乘公式具有以下性质:
- 对称性:C(n, k) = C(n, n-k)
- 递推关系:C(n+1, k) = C(n, k-1) + C(n, k)
- 与P的关系:C(n, k) = P(n, k) / k!,其中P(n, k)表示从n个元素中取出k个元素的排列数。
C阶乘公式的推导
C阶乘公式的推导基于排列的概念和阶乘的定义,我们知道从n个元素中取出k个元素的排列数为P(n, k),即n!/(n-k)!,由于组合不考虑顺序,我们需要将排列数除以k!以消除顺序的影响,从而得到组合数C(n, k),我们得到C阶乘公式:C(n, k) = n! / (k!(n-k)!)。
C阶乘公式的应用
- 组合计数:在统计和概率论中,我们经常需要计算不同事物的组合数,C阶乘公式为我们提供了计算这些组合数的有效方法。
- 概率计算:在概率计算中,许多概率问题可以转化为组合问题,通过使用C阶乘公式,我们可以方便地计算这些概率。
- 计算机科学:在计算机科学中,排列组合广泛应用于算法设计、数据结构等领域,C阶乘公式在计算算法的时间复杂度和空间复杂度时起着重要作用。
- 生物学:在生物学领域,C阶乘公式被广泛应用于计算基因组合、蛋白质相互作用等问题。
- 金融学:在金融学领域,C阶乘公式可用于计算投资组合的风险和收益,在计算投资组合的期望值时,我们需要计算不同资产组合的组合数,这时就可以使用C阶乘公式。
C阶乘公式作为排列组合中的重要工具,具有广泛的应用价值,通过本文的介绍,我们了解了C阶乘公式的定义、性质、推导及其在各个领域的应用,掌握C阶乘公式对于解决实际问题具有重要意义。

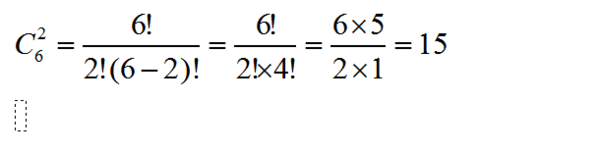
 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号